Introduction
Welcome to the se-lib User’s Guide with examples. The examples after the User’s Guide can be run separately from their cells, copied and pasted.
Installation
Run the cell below once at the beginning of each session to install the se-lib library. The from selib import * statement will import all its functions and classes to be called with no alias in the notebook.
!pip install -q se-lib
from selib import *
System Dynamics Modeling User’s Guide
Table of Contents
1. Overview
This manual provides an introduction and reference for modeling continuous systems using the se-lib Python package. se-lib supports the construction and simulation of system dynamics models using standard stock and flow structures using both procedural and object-oriented approaches. It adheres to the XMILE standard for system dynamics models and integrates with PySD for simulation execution. Models are compatible with Vensim and iThink/Stella tools using XMILE and MDL formats for importing and exporting.
The object-oriented interface is built around the SystemDynamicsModel class, enabling encapsulation of models, concurrent instantiation, and extensions of the model class. Users may also use the original procedural API for quick prototyping or compatibility with existing scripts. The procedural approach provides a more implicit modeling, but can be less flexible.
The manual includes reusable modeling templates, core system dynamics patterns such as goal-gap control and balancing loops, recommended modeling practices, detailed API documentation, and visual representations of feedback logic. It is suitable for a wide range of applications in systems thinking, behavioral simulation, engineering analysis, and education.
Detailed function references and more examples are available online at http://selib.org/function_reference.html#system-dynamics.
2. Getting Started with SE-Lib
To install the latest version of se-lib, use pip:
pip install se-lib
A system model is described by defining the standard elements for stocks (levels), flows (rates), and auxiliary constants or equations. Utility functions are available for equation formulation, data collection and displaying output.
Model construction begins by importing se-lib and initializing a model with the required time parameters. Simulations operate over a user-defined time horizon and return data as pandas DataFrames, which can be used for analysis and visualization.
from selib import *
init_sd_model(start=0, stop=30, dt=1)
Refer to Section 11 for a complete description of the modeling API.
3. Modeling Guidance and Tips
Modeling with se-lib requires attention to syntax, naming conventions, and logical structure. Names of model elements are specified as character strings and should not contain spaces; underscores (_) must be used to separate terms (e.g., Production_Rate). Variable names are case-sensitive and must exactly match those used in equations.
Equations are expressed as strings using standard arithmetic operators. Variables referenced in equations must already be defined within the model scope. The simulator does not check equations at entry time, so errors from undefined variables or misspellings will only become apparent at runtime.
Conditional statements can be expressed with logical constructs or, and, and not or the XMILE uppercase standards OR, AND, and NOT. The if_then_else(condition, value if true, value if false) or uppercase IF_THEN_ELSE(condition, value if true, value if false) are available.
Random number functions such as random() and random.uniform(a, b) are supported and internally translated into XMILE-compliant expressions. These generate new values at each timestep and are useful for modeling uncertainty or variability in external influences.
Time in se-lib is dimensionless. Modelers must maintain consistency in time unit interpretation (e.g., using all variables in units of days, months, etc.). Inconsistent use of time units can lead to misleading or invalid results.
The draw_model() function is recommended for verifying model structure prior to simulation. This visual representation helps ensure the correctness of stock-flow relationships and the presence of intended feedback loops.
4. Basic Modeling Patterns
4.1 Negative Feedback Loop
This classic balancing structure adjusts a level toward a target over time. It works by calculating the gap between a goal and the current level, then feeding a corrective flow in the direction that reduces this gap. The delay serves as a time constant, governing the speed of the system’s response. Over time, the level asymptotically approaches the goal value.
from selib import *
# negative feedback
init_sd_model(start=0, stop=5, dt=.1)
add_stock("level", 50, inflows=["rate"])
add_auxiliary("delay", .5)
add_auxiliary("goal", 100)
add_flow("rate", "(goal - level) / delay")
draw_model()
run_model()
plot_graph("level")

4.2 Exponential Growth
This reinforcing loop demonstrates positive feedback. The flow increases as the stock increases, which in turn further amplifies the flow. This results in exponential behavior and is frequently seen in unchecked population growth, viral spread, or compound interest.
from selib import *
# exponential growth
init_sd_model(start=0, stop=10, dt=.5)
add_stock("level", 100, inflows=["rate"])
add_auxiliary("growth_fraction", .8)
add_flow("rate", "growth_fraction * level")
draw_model()
run_model()
plot_graph('level')

4.3 Balancing Loop
A balancing loop with inventory control adjusts production to maintain a desired stock level. When inventory falls below target, production increases; when it’s above target, production slows. This loop exhibits goal-seeking behavior and helps stabilize system performance. External demand acts as an opposing outflow.
from selib import *
init_sd_model(0, 10, 1)
add_stock("Inventory", 50, inflows=["Production_Rate"], outflows=["Demand_Rate"])
add_auxiliary("Target_Inventory", 100)
add_auxiliary("Adj_Time", 4)
add_flow("Production_Rate", "(Target_Inventory - Inventory) / Adj_Time")
add_auxiliary("Demand", 10)
add_flow("Demand_Rate", "Demand")
draw_model()
run_model()
plot_graph(["Inventory", "Production_Rate"])

4.4 Goal-Gap Structure
This control structure reduces the deviation between a system’s state and a set point. A feedback signal (difference between goal and current value) is amplified by a gain factor and used to drive the stock toward the goal.
from selib import *
init_sd_model(0, 30, 1)
add_stock("Temperature", 20, inflows=["Heating"])
add_auxiliary("Set_Point", 22)
add_auxiliary("Gain", 1.5)
add_flow("Heating", "(Set_Point - Temperature) * Gain")
draw_model()
run_model()
plot_graph(["Temperature", "Set_Point"])

4.5 First-Order Delay
First-order delays represent lagged responses where a stock adjusts toward an input with exponential smoothing. The greater the delay time, the slower the convergence.
from selib import *
init_sd_model(0, 15, 1)
add_stock("Output", 0, inflows=["Flow"])
add_auxiliary("Input", 100)
add_auxiliary("Delay_Time", 5)
add_flow("Flow", "(Input - Output) / Delay_Time")
draw_model()
run_model()
plot_graph(["Input", "Output"])

4.6 Second-Order Delay
A second-order delay structure creates smoother responses by cascading two first-order delays. This is useful when modeling systems with inertia or buffer stages such as material transport, bureaucratic processes, or cognitive recognition lags.
from selib import *
init_sd_model(0, 30, 1)
add_stock("Stage1", 0, inflows=["Flow1"], outflows=["Flow2"])
add_stock("Stage2", 0, inflows=["Flow2"])
add_auxiliary("Input", 100)
add_auxiliary("DelayTime", 5)
add_flow("Flow1", "(Input - Stage1) / DelayTime")
add_flow("Flow2", "(Stage1 - Stage2) / DelayTime")
draw_model()
run_model()
plot_graph(["Stage1", "Stage2"])

…
5. Displaying Output
Upon execution of a system dynamics model, se-lib returns simulation results as a pandas.DataFrame object. This output contains the time-indexed values of all defined stocks, flows, and auxiliaries. The DataFrame facilitates further analysis, visualization, or export to external tools. The `run_model() function will execute a simulation and display a Pandas dataframe of the output. To execute a model and capture its output:
results = run_model()
Each column in the DataFrame corresponds to a model variable, and each row represents a timestep, as defined by the start, stop, and dt parameters provided during model initialization.
To inspect specific variables or values at particular timesteps, standard pandas indexing may be used:
results['Population'] # Full time series for Population
results['Births'][10] # Value of Births at the 10th timestep
results[['Population', 'Births']] # Multiple variables
This structured output enables direct integration with plotting functions, statistical analysis routines, or export mechanisms. All graphing and saving operations described in Section 6 operate directly on this result structure.
6. Graphing Functions
se-lib provides built-in graphing capabilities to visualize model outputs directly from the simulation results. These graphs are generated using the matplotlib library and support both single-variable and multi-variable plots.
Plotting to Screen
The plot_graph() function displays simulation results interactively. It supports multiple input formats: single variable names, separate arguments, or a list of variables.
plot_graph("Population")
plot_graph("Births", "Deaths")
plot_graph(["Population", "Births", "Deaths"])
When a list is used, variables are plotted together on a shared axis. When passed as separate arguments, they are displayed on individual subplots.
Saving to File
The save_graph() function saves output graphs to image files. The default format is PNG, and the format may be changed by modifying the filename extension.
save_graph("Population", filename="population_plot.png")
save_graph(["Births", "Deaths"], filename="flow_graph.svg")
Saved graphs are rendered as separate figures and written to disk, which is useful for reporting or presentation workflows. As with plotting, graphing functions operate on the output returned by run_model().
7. Random Number Functions
se-lib supports stochastic modeling using random number generation within auxiliary and flow equations. This allows the representation of uncertainty, noise, or nondeterministic behavior in the modeled system. In equations for auxiliaries and rates, the random number functions supported are called as if the following import has occurred: from random import random, random.uniform.
The random functions supported are:
random(): returns a new float uniformly distributed between 0 and 1 at each timestep.random.uniform(min, max): returns a new float uniformly distributed betweenminandmaxat each timestep.
These functions are automatically translated to XMILE-compatible expressions when the model is compiled for simulation. For xmile format compatibility, the functions RANDOM_0_1 and RANDOM_UNIFORM(min, max) are equivalent and also acceptable.
Example
The following example defines an auxiliary variable using random noise:
init_sd_model(start=0, stop=3, dt=.5)
add_auxiliary("random_parameter", "20*random()")
run_model()
( INITIAL TIME FINAL TIME TIME STEP SAVEPER random_parameter
0.0 0 3 0.5 0.5 0.087466
0.5 0 3 0.5 0.5 11.174929
1.0 0 3 0.5 0.5 13.506344
1.5 0 3 0.5 0.5 4.342211
2.0 0 3 0.5 0.5 5.449781
2.5 0 3 0.5 0.5 7.323554
3.0 0 3 0.5 0.5 17.220789,
Each timestep generates a new random value for Stochastic_Input, producing a non-repeating time series. It is important to note that random values are recomputed each time the model is run, and results may vary unless reproducibility measures (e.g., seeding) are implemented outside SE-Lib.
8. Utility and Test Functions
Standard test functions are available for pulse, ramp and step inputs as shown below. The full set of functions available in PySD can be used but have not all been tested.
init_sd_model(0, 10, 1)
add_stock("Level", 0, inflows=["Pulse", "Ramp"])
add_flow("Pulse", "pulse(100, 2)")
add_flow("Ramp", "ramp(3, 5)")
run_model()
plot_graph("Pulse", "Ramp", "Level")
9. Advanced Usage
9.1 Extending a Model Instance
Create a new class that extends a population model by adding carrying capacity with the following.
class PopulationWithCapacityModel(SystemDynamicsModel):
def __init__(self, start, stop, dt, initial_population, carrying_capacity):
super().__init__(start, stop, dt)
self.add_stock("Population", initial=initial_population, inflows=["Births"], outflows=["Deaths"])
self.add_auxiliary("BirthRate", equation=0.02)
self.add_auxiliary("CarryingCapacity", equation=carrying_capacity)
self.add_auxiliary("CrowdingEffect", equation="Population / CarryingCapacity")
self.add_auxiliary("EffectiveGrowthRate", equation="BirthRate * (1 - CrowdingEffect)")
self.add_flow("Births", equation="Population * EffectiveGrowthRate")
self.add_auxiliary("DeathRate", equation=0.01)
self.add_flow("Deaths", equation="Population * DeathRate") # Keep a simple death rate
# Create an instance of the extended model
population_capacity_model = PopulationWithCapacityModel(start=0, stop=200, dt=1, initial_population=50, carrying_capacity=500)
9.1 PySD Integration
SE-Lib is fully compatible with PySD. Any PySD function or supported XMILE structure may be used where appropriate. See PySD Docs for advanced formulations.
10. Appendix A - Function Reference
The following functions and methods define the modeling API for se-lib. All functions can be used in either procedural or object-oriented workflows.
init_sd_model(start, stop, dt, stop_when=None)
Initializes a new system dynamics model over the specified simulation time frame.
Args: - start (float): Start time of the simulation. - stop (float): End time of the simulation. - dt (float): Time step for numerical integration. - stop_when (float): Logical condition using model variables to stop the simulation.
Returns: - SystemDynamicsModel instance
Example:
init_sd_model(start=0, stop=50, dt=1.0)
Examples with stop_when:
init_sd_model(start=0, stop=50, dt=1.0, stop_when("stock1 >= 100")
init_sd_model(start=0, stop=50, dt=1.0, stop_when("stock1 >= 100 or stock2 >=80")
add_stock(name, initial, inflows=[], outflows=[])
Adds a stock variable (level) to the system dynamics model.
Args: - name (str): Name of the stock. - initial (float): Initial value of the stock. - inflows (list, optional): Names of inflow variables affecting this stock. - outflows (list, optional): Names of outflow variables affecting this stock.
Returns: - None
Example:
add_stock("Population", initial=100, inflows=["Births"], outflows=["Deaths"])
add_flow(name, equation)
Defines a flow (rate of change) for use in stock updates.
Args: - name (str): Name of the flow. - equation (str): Equation as a string to compute the flow value.
Returns: - None
Example:
add_flow("Births", "Birth_Rate * Population")
add_auxiliary(name, equation)
Defines an auxiliary variable or constant used in the model.
Args: - name (str): Name of the auxiliary variable. - equation (str): String representation of the equation or constant value.
Returns: - None
Example:
add_auxiliary("Birth_Rate", "0.02")
add_auxiliary_lookup(name, input, xpoints, ypoints)
Creates a lookup function for a nonlinear relationship.
Args: - name (str): Name of the auxiliary variable. - input (str): Name of the input variable used in the lookup. - xpoints (list): List of input values (x-axis). - ypoints (list): List of output values (y-axis).
Returns: - None
Example:
add_auxiliary_lookup("Saturation", "Population", [0, 1000, 2000], [1, 0.5, 0.1])
plot_graph(*outputs)
Plots model results using matplotlib.
Args: - *outputs (str or list): Names of variables to plot (e.g., “Population”, [“Births”, “Deaths”]).
Returns: - None
Example:
plot_graph("Population")
plot_graph(["Births", "Deaths"])
save_graph(*outputs, filename='graph.png')
Saves a plot of the simulation
draw_sd_model(filename=None, format=’svg’)
Generates and renders a visual system dynamics model diagram using Graphviz.
get_stop_time()
Returns the logical end time based on a stop_when condition.
get_model_structure()
Returns a dictionary of model components (stocks, flows, auxiliaries).
Examples
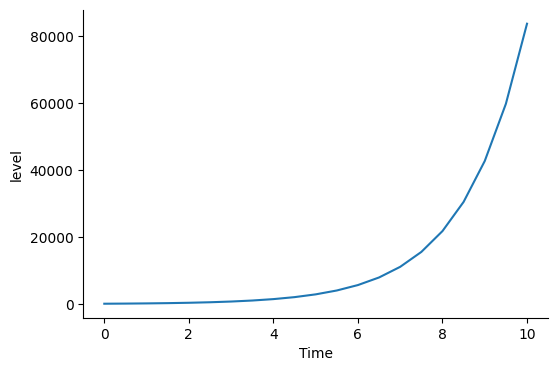
Exponential Growth
from selib import *
# exponential_growth
init_sd_model(start=0, stop=10, dt=.5)
add_stock("level", 100, inflows=["rate"])
add_auxiliary("growth_fraction", .8)
add_flow("rate", "growth_fraction * level")
draw_model()
run_model()
save_graph('level', filename="exponential_growth.png")
--------------
INITIAL TIME FINAL TIME TIME STEP SAVEPER growth_fraction \
time
0.0 0 10 0.5 0.5 0.8
0.5 0 10 0.5 0.5 0.8
1.0 0 10 0.5 0.5 0.8
1.5 0 10 0.5 0.5 0.8
2.0 0 10 0.5 0.5 0.8
2.5 0 10 0.5 0.5 0.8
3.0 0 10 0.5 0.5 0.8
3.5 0 10 0.5 0.5 0.8
4.0 0 10 0.5 0.5 0.8
4.5 0 10 0.5 0.5 0.8
5.0 0 10 0.5 0.5 0.8
5.5 0 10 0.5 0.5 0.8
6.0 0 10 0.5 0.5 0.8
6.5 0 10 0.5 0.5 0.8
7.0 0 10 0.5 0.5 0.8
7.5 0 10 0.5 0.5 0.8
8.0 0 10 0.5 0.5 0.8
8.5 0 10 0.5 0.5 0.8
9.0 0 10 0.5 0.5 0.8
9.5 0 10 0.5 0.5 0.8
10.0 0 10 0.5 0.5 0.8
rate level
time
0.0 80.000000 100.000000
0.5 112.000000 140.000000
1.0 156.800000 196.000000
1.5 219.520000 274.400000
2.0 307.328000 384.160000
2.5 430.259200 537.824000
3.0 602.362880 752.953600
3.5 843.308032 1054.135040
4.0 1180.631245 1475.789056
4.5 1652.883743 2066.104678
5.0 2314.037240 2892.546550
5.5 3239.652136 4049.565170
6.0 4535.512990 5669.391238
6.5 6349.718186 7937.147733
7.0 8889.605460 11112.006826
7.5 12445.447645 15556.809556
8.0 17423.626702 21779.533378
8.5 24393.077383 30491.346729
9.0 34150.308337 42687.885421
9.5 47810.431672 59763.039589
10.0 66934.604340 83668.255425
--------------
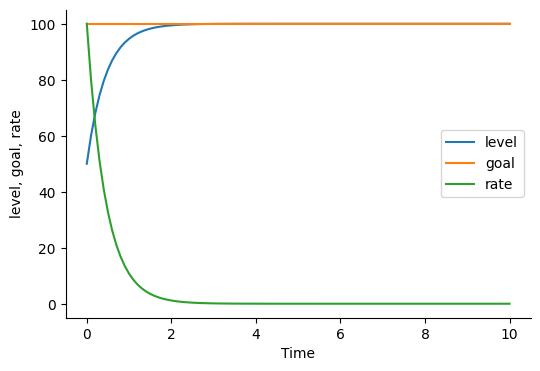
Negative Feedback
# negative feedback
from selib import *
init_sd_model(start=0, stop=10, dt=.1)
add_stock("level", 50, inflows=["rate"])
add_auxiliary("delay", .5)
add_auxiliary("goal", 100)
add_flow("rate", "(goal - level) / delay")
draw_model()
run_model()
save_graph(['level', 'goal', 'rate'], filename="negative_feedback.svg")
--------------
INITIAL TIME FINAL TIME TIME STEP SAVEPER delay goal rate \
time
0.0 0 10 0.1 0.1 0.5 100 1.000000e+02
0.1 0 10 0.1 0.1 0.5 100 8.000000e+01
0.2 0 10 0.1 0.1 0.5 100 6.400000e+01
0.3 0 10 0.1 0.1 0.5 100 5.120000e+01
0.4 0 10 0.1 0.1 0.5 100 4.096000e+01
... ... ... ... ... ... ... ...
9.6 0 10 0.1 0.1 0.5 100 4.973231e-08
9.7 0 10 0.1 0.1 0.5 100 3.978585e-08
9.8 0 10 0.1 0.1 0.5 100 3.182868e-08
9.9 0 10 0.1 0.1 0.5 100 2.546295e-08
10.0 0 10 0.1 0.1 0.5 100 2.037035e-08
level
time
0.0 50.00
0.1 60.00
0.2 68.00
0.3 74.40
0.4 79.52
... ...
9.6 100.00
9.7 100.00
9.8 100.00
9.9 100.00
10.0 100.00
[101 rows x 8 columns]
--------------
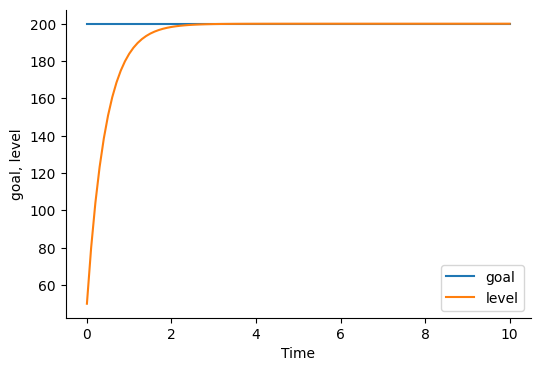
Goal Seeking Behavior
from selib import *
# goal seeking behavior with negative feedback
init_sd_model(start=0, stop=10, dt=.1)
add_stock("level", 50, inflows=["rate"])
add_auxiliary("time_constant", .5)
add_auxiliary("goal", 200)
add_flow("rate", "(goal - level) / time_constant")
draw_model()
run_model()
plot_graph(['goal', 'level'])
--------------
INITIAL TIME FINAL TIME TIME STEP SAVEPER time_constant goal \
time
0.0 0 10 0.1 0.1 0.5 200
0.1 0 10 0.1 0.1 0.5 200
0.2 0 10 0.1 0.1 0.5 200
0.3 0 10 0.1 0.1 0.5 200
0.4 0 10 0.1 0.1 0.5 200
... ... ... ... ... ... ...
9.6 0 10 0.1 0.1 0.5 200
9.7 0 10 0.1 0.1 0.5 200
9.8 0 10 0.1 0.1 0.5 200
9.9 0 10 0.1 0.1 0.5 200
10.0 0 10 0.1 0.1 0.5 200
rate level
time
0.0 3.000000e+02 50.00
0.1 2.400000e+02 80.00
0.2 1.920000e+02 104.00
0.3 1.536000e+02 123.20
0.4 1.228800e+02 138.56
... ... ...
9.6 1.491970e-07 200.00
9.7 1.193576e-07 200.00
9.8 9.548609e-08 200.00
9.9 7.638886e-08 200.00
10.0 6.111111e-08 200.00
[101 rows x 8 columns]
--------------
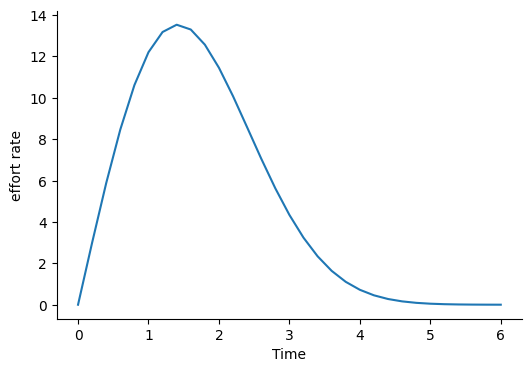
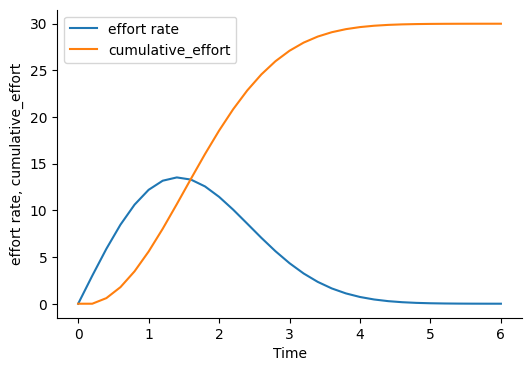
Rayleigh Curve Staffing
# Rayleigh Curve Staffing
from selib import *
init_sd_model(start=0, stop=6, dt=.2)
add_stock("cumulative_effort", 0, inflows=["effort rate"])
add_flow("effort rate",
"learning_function * (estimated_total_effort - cumulative_effort)")
add_auxiliary("learning_function", "manpower_buildup_parameter * time")
add_auxiliary("manpower_buildup_parameter", .5)
add_auxiliary("estimated_total_effort", 30)
draw_model()
run_model()
save_graph("effort rate", filename="rayleigh_curve_effort_rate.png")
save_graph(["effort rate", "cumulative_effort"],
filename="rayleigh_curve_components.png")
--------------
INITIAL TIME FINAL TIME TIME STEP SAVEPER learning_function \
time
0.0 0 6 0.2 0.2 0.0
0.2 0 6 0.2 0.2 0.1
0.4 0 6 0.2 0.2 0.2
0.6 0 6 0.2 0.2 0.3
0.8 0 6 0.2 0.2 0.4
1.0 0 6 0.2 0.2 0.5
1.2 0 6 0.2 0.2 0.6
1.4 0 6 0.2 0.2 0.7
1.6 0 6 0.2 0.2 0.8
1.8 0 6 0.2 0.2 0.9
2.0 0 6 0.2 0.2 1.0
2.2 0 6 0.2 0.2 1.1
2.4 0 6 0.2 0.2 1.2
2.6 0 6 0.2 0.2 1.3
2.8 0 6 0.2 0.2 1.4
3.0 0 6 0.2 0.2 1.5
3.2 0 6 0.2 0.2 1.6
3.4 0 6 0.2 0.2 1.7
3.6 0 6 0.2 0.2 1.8
3.8 0 6 0.2 0.2 1.9
4.0 0 6 0.2 0.2 2.0
4.2 0 6 0.2 0.2 2.1
4.4 0 6 0.2 0.2 2.2
4.6 0 6 0.2 0.2 2.3
4.8 0 6 0.2 0.2 2.4
5.0 0 6 0.2 0.2 2.5
5.2 0 6 0.2 0.2 2.6
5.4 0 6 0.2 0.2 2.7
5.6 0 6 0.2 0.2 2.8
5.8 0 6 0.2 0.2 2.9
6.0 0 6 0.2 0.2 3.0
manpower_buildup_parameter estimated_total_effort effort rate \
time
0.0 0.5 30 0.000000
0.2 0.5 30 3.000000
0.4 0.5 30 5.880000
0.6 0.5 30 8.467200
0.8 0.5 30 10.612224
1.0 0.5 30 12.204058
1.2 0.5 30 13.180382
1.4 0.5 30 13.531859
1.6 0.5 30 13.299884
1.8 0.5 30 12.568391
2.0 0.5 30 11.451200
2.2 0.5 30 10.077056
2.4 0.5 30 8.574659
2.6 0.5 30 7.059802
2.8 0.5 30 5.626120
3.0 0.5 30 4.340149
3.2 0.5 30 3.240645
3.4 0.5 30 2.341366
3.6 0.5 30 1.636202
3.8 0.5 30 1.105345
4.0 0.5 30 0.721383
4.2 0.5 30 0.454471
4.4 0.5 30 0.276145
4.6 0.5 30 0.161671
4.8 0.5 30 0.091098
5.0 0.5 30 0.049345
5.2 0.5 30 0.025659
5.4 0.5 30 0.012790
5.6 0.5 30 0.006101
5.8 0.5 30 0.002780
6.0 0.5 30 0.001208
cumulative_effort
time
0.0 0.000000
0.2 0.000000
0.4 0.600000
0.6 1.776000
0.8 3.469440
1.0 5.591885
1.2 8.032696
1.4 10.668773
1.6 13.375145
1.8 16.035121
2.0 18.548800
2.2 20.839040
2.4 22.854451
2.6 24.569383
2.8 25.981343
3.0 27.106567
3.2 27.974597
3.4 28.622726
3.6 29.090999
3.8 29.418239
4.0 29.639308
4.2 29.783585
4.4 29.874479
4.6 29.929708
4.8 29.962043
5.0 29.980262
5.2 29.990131
5.4 29.995263
5.6 29.997821
5.8 29.999041
6.0 29.999597
--------------
--------------
Random Functions and Measuring Stop Time
This example illustrates measuring elapsed simulation time using the stop_when initialization parameter and get_stop_time() function. It captures the project end when staffing effort rate goes to zero.
from selib import *
init_sd_model(start=0, stop=6, dt=.2, stop_when="effort_rate <= 0")
add_stock("cumulative_effort", 0, inflows=["effort rate"])
add_flow("effort_rate",
"learning_function * (estimated_total_effort - cumulative_effort)")
add_auxiliary("learning_function", "manpower_buildup_parameter * time")
add_auxiliary("manpower_buildup_parameter", 'random.uniform(.2, .7)')
add_auxiliary("estimated_total_effort", 'random.uniform(25, 35)')
run_model()
print(f"Project end time is {get_stop_time()}")
Simulation ends at time = 3.0
INITIAL TIME FINAL TIME TIME STEP SAVEPER learning_function \
time
0.0 0 6 0.2 0.2 0.000000
0.2 0 6 0.2 0.2 0.122395
0.4 0 6 0.2 0.2 0.235581
0.6 0 6 0.2 0.2 0.206761
0.8 0 6 0.2 0.2 0.304143
1.0 0 6 0.2 0.2 0.207023
1.2 0 6 0.2 0.2 0.459536
1.4 0 6 0.2 0.2 0.320776
1.6 0 6 0.2 0.2 0.781662
1.8 0 6 0.2 0.2 0.851055
2.0 0 6 0.2 0.2 1.260378
2.2 0 6 0.2 0.2 1.045175
2.4 0 6 0.2 0.2 1.072665
2.6 0 6 0.2 0.2 1.511612
2.8 0 6 0.2 0.2 1.299925
3.0 0 6 0.2 0.2 1.825976
manpower_buildup_parameter estimated_total_effort effort_rate \
time
0.0 0.682189 34.323998 0.000000
0.2 0.611974 27.620483 3.380603
0.4 0.588953 30.330142 6.985926
0.6 0.344601 29.166838 5.601875
0.8 0.380179 33.010074 9.068448
1.0 0.207023 31.018010 5.384799
1.2 0.382947 32.624585 12.196203
1.4 0.229126 28.600847 6.440316
1.6 0.488538 30.481037 16.156478
1.8 0.472808 29.680247 14.159276
2.0 0.630189 31.585909 19.801960
2.2 0.475079 25.422697 5.839935
2.4 0.446944 31.348129 11.096682
2.6 0.581389 29.838478 10.000791
2.8 0.464259 30.166600 6.426755
3.0 0.608659 25.307849 -2.191463
cumulative_effort
time
0.0 0.000000
0.2 0.000000
0.4 0.676121
0.6 2.073306
0.8 3.193681
1.0 5.007370
1.2 6.084330
1.4 8.523571
1.6 9.811634
1.8 13.042930
2.0 15.874785
2.2 19.835177
2.4 21.003164
2.6 23.222500
2.8 25.222658
3.0 26.508009
Project end time is 3.0
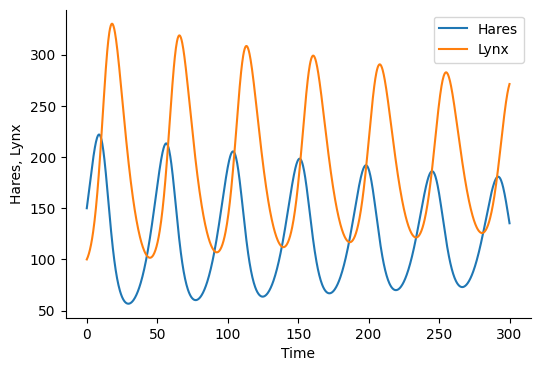
Predator Prey Model
# Predator Prey Model with Carrying Capacity
import selib as se
# Initialize model
init_sd_model(start=0, stop=300, dt=0.25)
# Auxiliaries
add_auxiliary_lookup("Carrying_Capacity_Effect", "Hares",
["0, 500, 1000, 1500, 2000"], ["1, .8, .5, .2, .05"])
add_auxiliary("Hare_Growth_Rate", "0.162 * Carrying_Capacity_Effect")
add_auxiliary("Hare_Death_Rate", ".0008 * Lynx")
add_auxiliary("Lynx_Death_Rate", "0.12")
add_auxiliary("Lynx_Birth_Rate", "0.001 * Hares")
# Stocks
add_stock("Hares", "150", inflows=["Hare_Births"], outflows=["Hare_Deaths"])
add_stock("Lynx", "100", inflows=["Lynx_Births"], outflows=["Lynx_Deaths"])
# Flows
add_flow("Hare_Births", "Hare_Growth_Rate * Hares")
add_flow("Hare_Deaths", "Hare_Death_Rate * Hares")
add_flow("Lynx_Births", "Lynx_Birth_Rate * Lynx")
add_flow("Lynx_Deaths", "Lynx_Death_Rate * Lynx")
d = draw_model_diagram(filename="sd")
results = run_model()
save_graph(["Hares", "Lynx"])
--------------
INITIAL TIME FINAL TIME TIME STEP SAVEPER \
time
0.00 0 300 0.25 0.25
0.25 0 300 0.25 0.25
0.50 0 300 0.25 0.25
0.75 0 300 0.25 0.25
1.00 0 300 0.25 0.25
... ... ... ... ...
299.00 0 300 0.25 0.25
299.25 0 300 0.25 0.25
299.50 0 300 0.25 0.25
299.75 0 300 0.25 0.25
300.00 0 300 0.25 0.25
Carrying_Capacity_Effect Hare_Growth_Rate Hare_Death_Rate \
time
0.00 0.940000 0.152280 0.080000
0.25 0.938916 0.152104 0.080600
0.50 0.937824 0.151927 0.081259
0.75 0.936725 0.151750 0.081979
1.00 0.935622 0.151571 0.082762
... ... ... ...
299.00 0.942403 0.152669 0.212617
299.25 0.943266 0.152809 0.213893
299.50 0.944132 0.152949 0.215060
299.75 0.945000 0.153090 0.216118
300.00 0.945866 0.153230 0.217063
Lynx_Death_Rate Lynx_Birth_Rate Hare_Births Hare_Deaths \
time
0.00 0.12 0.150000 22.842000 12.000000
0.25 0.12 0.152710 23.227933 12.308466
0.50 0.12 0.155440 23.615661 12.630947
0.75 0.12 0.158187 24.004731 12.967987
1.00 0.12 0.160946 24.394660 13.320143
... ... ... ... ...
299.00 0.12 0.143993 21.983347 30.615492
299.25 0.12 0.141835 21.673716 30.337545
299.50 0.12 0.139669 21.362341 30.037341
299.75 0.12 0.137501 21.049955 29.716338
300.00 0.12 0.135334 20.737271 29.376063
Lynx_Births Lynx_Deaths Hares Lynx
time
0.00 15.000000 12.000000 150.000000 100.000000
0.25 15.385583 12.090000 152.710500 100.750000
0.50 15.788684 12.188867 155.440367 101.573896
0.75 16.209984 12.296862 158.186545 102.473850
1.00 16.650179 12.414256 160.945731 103.452130
... ... ... ... ...
299.00 38.269365 31.892621 143.993301 265.771845
299.25 37.921932 32.083924 141.835264 267.366031
299.50 37.546676 32.259064 139.669307 268.825533
299.75 37.145423 32.417692 137.500557 270.147436
300.00 36.720078 32.559524 135.333961 271.329369
[1201 rows x 15 columns]
--------------
# patch to increase padding for model diagrams
import graphviz
# Store original methods
_original_digraph_init = graphviz.Digraph.__init__
def patched_digraph_init(self, *args, **kwargs):
_original_digraph_init(self, *args, **kwargs)
# Apply defaults
self.attr('graph', pad='1')
# Apply patches
graphviz.Digraph.__init__ = patched_digraph_init
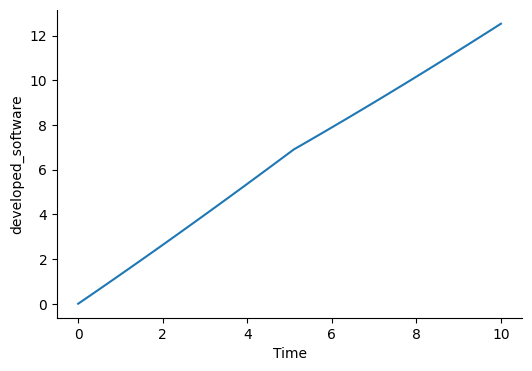
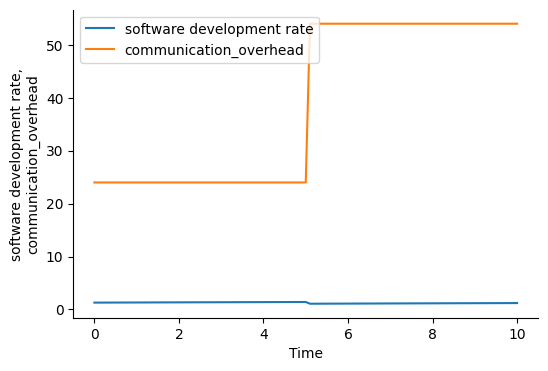
Brooks’s Law Model
# Brooks's Law Model
from selib import *
init_sd_model(start=0, stop=10, dt=.1)
add_stock("requirements", 500, inflows=[], outflows=["software development rate"])
add_stock("developed_software", 0, inflows=["software development rate"])
add_flow("software development rate", "nominal_productivity*(1.-communication_overhead/100.)*(.8*new_project_personnel+1.2*(experienced_personnel-experienced_personnel_needed_for_training))")
add_stock("experienced_personnel", 10.0, inflows=["assimilation rate"])
add_stock("new_project_personnel", 10.0, inflows=["people_added"], outflows=["assimilation rate"])
add_flow("assimilation rate", "new_project_personnel/20")
add_flow("people_added", "pulse(10,5)")
add_auxiliary("nominal_productivity", .1)
add_auxiliary("training_overhead_FTE_experienced", 25.)
add_auxiliary("experienced_personnel_needed_for_training", "new_project_personnel*training_overhead_FTE_experienced/100.")
add_auxiliary_lookup("communication_overhead", "experienced_personnel + new_project_personnel",
["0, 5, 10, 15, 20, 25, 30"], ["0, 1.5, 6, 13.5, 24, 37.5, 54"])
draw_sd_model()
output = run_model()
plot_graph("developed_software")
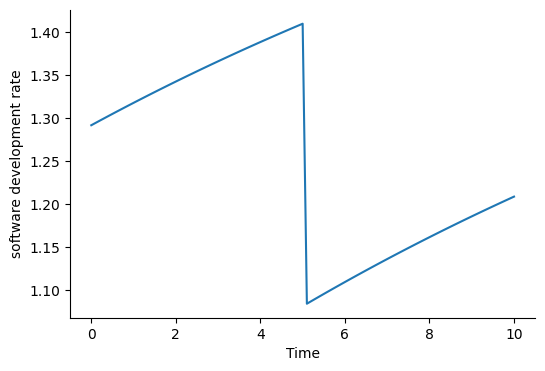
plot_graph("software development rate")
plot_graph(["software development rate", "communication_overhead"])
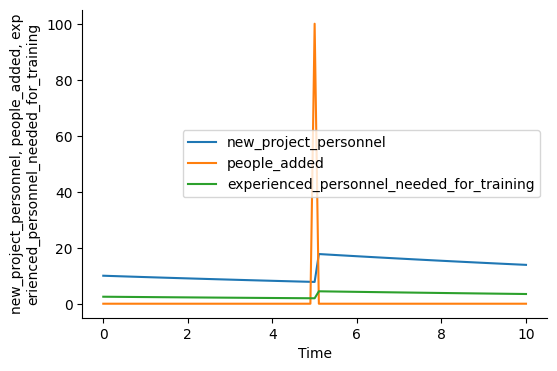
plot_graph(["new_project_personnel", "people_added", "experienced_personnel_needed_for_training"])
--------------
INITIAL TIME FINAL TIME TIME STEP SAVEPER nominal_productivity \
time
0.0 0 10 0.1 0.1 0.1
0.1 0 10 0.1 0.1 0.1
0.2 0 10 0.1 0.1 0.1
0.3 0 10 0.1 0.1 0.1
0.4 0 10 0.1 0.1 0.1
... ... ... ... ... ...
9.6 0 10 0.1 0.1 0.1
9.7 0 10 0.1 0.1 0.1
9.8 0 10 0.1 0.1 0.1
9.9 0 10 0.1 0.1 0.1
10.0 0 10 0.1 0.1 0.1
training_overhead_FTE_experienced \
time
0.0 25.0
0.1 25.0
0.2 25.0
0.3 25.0
0.4 25.0
... ...
9.6 25.0
9.7 25.0
9.8 25.0
9.9 25.0
10.0 25.0
experienced_personnel_needed_for_training communication_overhead \
time
0.0 2.500000 24.0
0.1 2.487500 24.0
0.2 2.475062 24.0
0.3 2.462687 24.0
0.4 2.450374 24.0
... ... ...
9.6 3.540261 54.0
9.7 3.522560 54.0
9.8 3.504947 54.0
9.9 3.487422 54.0
10.0 3.469985 54.0
software development rate assimilation rate people_added \
time
0.0 1.292000 0.500000 0.0
0.1 1.294660 0.497500 0.0
0.2 1.297307 0.495012 0.0
0.3 1.299940 0.492537 0.0
0.4 1.302560 0.490075 0.0
... ... ... ...
9.6 1.200014 0.708052 0.0
9.7 1.202294 0.704512 0.0
9.8 1.204563 0.700989 0.0
9.9 1.206820 0.697484 0.0
10.0 1.209066 0.693997 0.0
requirements developed_software experienced_personnel \
time
0.0 500.000000 0.000000 10.000000
0.1 499.870800 0.129200 10.050000
0.2 499.741334 0.258666 10.099750
0.3 499.611603 0.388397 10.149251
0.4 499.481609 0.518391 10.198505
... ... ... ...
9.6 487.953319 12.046681 15.838955
9.7 487.833317 12.166683 15.909760
9.8 487.713088 12.286912 15.980211
9.9 487.592632 12.407368 16.050310
10.0 487.471950 12.528050 16.120059
new_project_personnel
time
0.0 10.000000
0.1 9.950000
0.2 9.900250
0.3 9.850749
0.4 9.801495
... ...
9.6 14.161045
9.7 14.090240
9.8 14.019789
9.9 13.949690
10.0 13.879941
[101 rows x 15 columns]
--------------
--------------
--------------
--------------
--------------
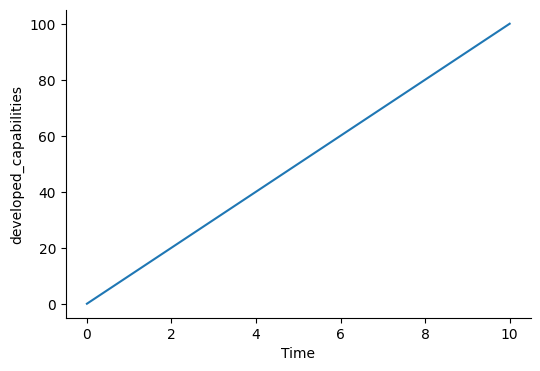
Object Oriented Simulation Using Classes
# @title Capability Development Model with Stop Condition
from selib import *
# Initialize SystemDynamicsModel model instance
model = SystemDynamicsModel(start=0, stop=25, dt=0.1, stop_when="developed_capabilities >= 100")
model.add_stock(name="capabilities_to_do", initial=100, outflows=["development_rate"])
model.add_stock(name="developed_capabilities", initial=0, inflows=["development_rate"])
model.add_flow(name="development_rate", equation="IF capabilities_to_do > 0 THEN 10 ELSE 0")
# Draw the model diagram
model.draw_model()
# Run the model simulation
results = model.run_model()
# Plot the 'developed_capabilities'
model.plot_graph('developed_capabilities')
# Print the stop time
stop_time = model.get_stop_time()
print(f'stop time = {stop_time}')
--------------
Simulation ends at time = 10.0
INITIAL TIME FINAL TIME TIME STEP SAVEPER development_rate \
time
0.0 0 25 0.1 0.1 10
0.1 0 25 0.1 0.1 10
0.2 0 25 0.1 0.1 10
0.3 0 25 0.1 0.1 10
0.4 0 25 0.1 0.1 10
... ... ... ... ... ...
9.6 0 25 0.1 0.1 10
9.7 0 25 0.1 0.1 10
9.8 0 25 0.1 0.1 10
9.9 0 25 0.1 0.1 10
10.0 0 25 0.1 0.1 0
capabilities_to_do developed_capabilities
time
0.0 100.0 0.0
0.1 99.0 1.0
0.2 98.0 2.0
0.3 97.0 3.0
0.4 96.0 4.0
... ... ...
9.6 4.0 96.0
9.7 3.0 97.0
9.8 2.0 98.0
9.9 1.0 99.0
10.0 0.0 100.0
[101 rows x 7 columns]
--------------
stop time = 10.0
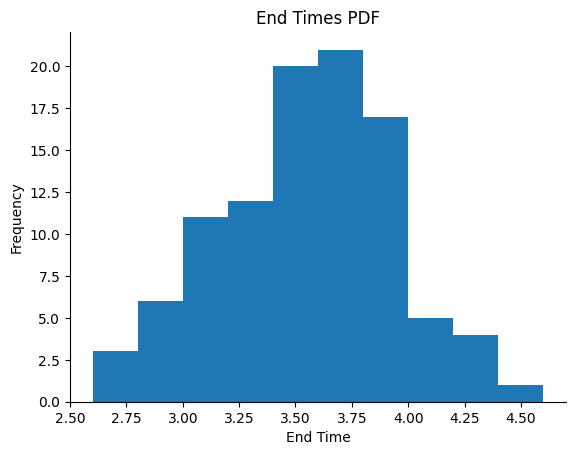
Monte Carlo Simulation and Output Analysis
# Monte Carlo simulation for Rayleigh Curve Staffing and end time output analysis
from selib import *
import numpy as np
number_runs = 100
# vary manpower_buildup_parameter and estimated_total_effort in model definition
end_times = [] # initialize output data list
for run in range(number_runs):
init_sd_model(start=0, stop=6, dt=.2, stop_when="effort_rate <=0")
add_stock("cumulative_effort", 0, inflows=["effort rate"])
add_flow(
"effort_rate",
"learning_function * (estimated_total_effort - cumulative_effort)")
add_auxiliary("learning_function", "manpower_buildup_parameter * time")
add_auxiliary("manpower_buildup_parameter", 'random.uniform(.2, .7)')
add_auxiliary("estimated_total_effort", f'random.uniform(25, 35)')
run_model(verbose=False)
end_times.append(get_stop_time())
print(f'End Time Mean for {number_runs} runs = ', np.mean(end_times))
# PDF histogram with Matplotlib
fig, axis = plt.subplots()
axis.hist(end_times)
axis.set(title=f'End Times PDF', xlabel='End Time', ylabel='Frequency')
plt.savefig(f"end_times_PDF")
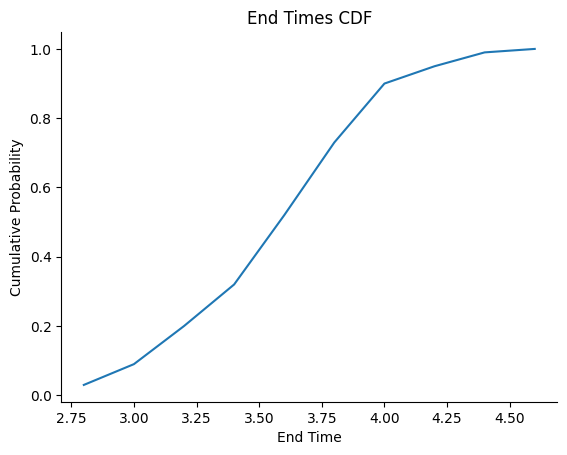
# CDF with NumPy and Matplotlib
fig, axis = plt.subplots()
# Use the histogram function to bin the data
histogram_bin_counts, bin_edges = np.histogram (end_times, density=True)
cdf = np.cumsum (histogram_bin_counts)
axis.plot (bin_edges[1:], cdf/cdf[-1])
axis.set(title=f'End Times CDF', xlabel='End Time', ylabel='Cumulative Probability')
plt.savefig(f"end_times_CDF")
End Time Mean for 100 runs = 3.4560000000000004
--------------
--------------
Special Functions
from selib import *
init_sd_model(start=0, stop=6, dt=.2, stop_when="effort_rate <= 0")
add_stock("cumulative_effort", 0, inflows=["effort rate"])
add_flow("effort_rate",
"learning_function * (estimated_total_effort - cumulative_effort)")
add_auxiliary("learning_function", "manpower_buildup_parameter * time")
add_auxiliary("manpower_buildup_parameter", 'random.uniform(.2, .7)')
add_auxiliary("estimated_total_effort", 'random.uniform(25, 35)')
run_model()
print(f"Project end time is {get_stop_time()}")
Stop When Condition
# demonstrate stop_when condition to end simulation and the get_stop function
# collect time when the stock reaches zero
from selib import *
init_sd_model(start=0, stop=10, dt=.5, stop_when="stock <= 0")
add_stock("stock", 50, outflows=["outflow_rate"])
add_flow("outflow_rate", "20")
run_model()
print('stop time = ', get_stop_time())
Simulation ends at time = 2.5
INITIAL TIME FINAL TIME TIME STEP SAVEPER outflow_rate stock
time
0.0 0 10 0.5 0.5 20 50.0
0.5 0 10 0.5 0.5 20 40.0
1.0 0 10 0.5 0.5 20 30.0
1.5 0 10 0.5 0.5 20 20.0
2.0 0 10 0.5 0.5 20 10.0
2.5 0 10 0.5 0.5 20 0.0
stop time = 2.5
If Then Else
# demonstrate if then else function
from selib import *
init_sd_model(start=0, stop=5, dt=1)
# set conditional variable
# if time > 2 then 1 else 0
add_auxiliary("conditional", "if_then_else(time > 2, 1, 0)")
add_auxiliary("conditional2", "if_then_else(time < 4, .5, .7)")
run_model()
INITIAL TIME FINAL TIME TIME STEP SAVEPER conditional conditional2
time
0 0 5 1 1 0 0.5
1 0 5 1 1 0 0.5
2 0 5 1 1 0 0.5
3 0 5 1 1 1 0.5
4 0 5 1 1 1 0.7
5 0 5 1 1 1 0.7
INITIAL TIME FINAL TIME TIME STEP SAVEPER conditional conditional2
time
0 0 5 1 1 0 0.5
1 0 5 1 1 0 0.5
2 0 5 1 1 0 0.5
3 0 5 1 1 1 0.5
4 0 5 1 1 1 0.7
5 0 5 1 1 1 0.7